投稿者: southbook

６０は明らかにサボってるよねぇ

じゃぁ８０は？
１００は？１２０？は？

あなたの”１００”と私の「１００」は違うということに
気が付かなければならない

あと、

界隈でよく謂う「頑張らなくていい」は、頑張らないヒトの言い訳に使われてはならない

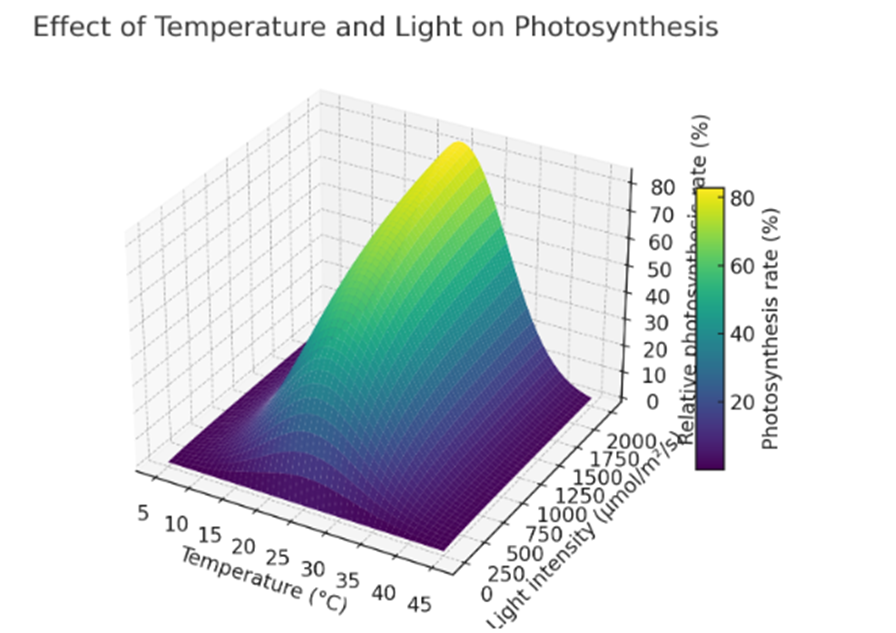
ん～？　この業界、詰まる所

正規分布とシグモイド関数、三角関数の適用し処が体得できてれば

とりま現場レベルでは勝ち確なのではなかろうか…

求めよさらば与えられん

先人曰く、

求めなさい。そうすれば、与えられるであろう。探しなさい。そうすれば、見いだすであろう。門をたたきなさい。そうすれば、開かれるであろう。（マタイ7:7）

「求める」のが先。かつ「正しく」が抜けてて。

卒啄同時

「正しく」「求める」のが先にたつと解釈する。極めて「同時」とみなせる程度に「求める」ほうが先なら理想的ｗ

指導者は「同時」という言葉の解釈を見誤るな。価値観の押し付けや詰め込みが正しい教育・指導ではない。　当然に学習者のレベルにも依るが、指導的立場の者に必要な能力は観察力と段取り力。学習者の興味ある方向を見定め、その殻が薄いところ突付いて教えて誘導してやるのが指導者の真の価値。学習者は自分で勝手に殻を破って次のステージに進む。

愛とは興味・関心

「愛の反対は無関心」からの当然の帰結。

好き嫌いではなく、興味関心。
この解釈であれば、親兄弟・隣人・世界・機械・仕事・推し活…etc　対象が何だって適用できるし、生きてる限り無料で無限に湧くモノじゃね？　コレこそまさに神の所業（永久機関）と言っとけば（解釈しとけば）よくて。誰も困らん。

「好きの延長」が愛でなければならないと思うからしんどくなるのであって、興味関心だと思えば、別に対象が敵でも嫌いでも大丈夫。勝手に無限に湧けばいい。　簡単。

ただ、対象が「好き」であれば（あり続ければ）、対象への理解は早く深いってだけの話。　簡単。

様々な「興味関心」が寄り集まって世の中が形成されるなら、世界は発展する方向に進むしかないんじゃね？　簡単。　って宗教（少なくともキリスト教と仏教の、素人解釈で）は言っているようにしか見えんのだが。

結論

学習者は、「興味関心」を持ち、正しく問うのが使命。

教育者は、学習者の興味関心を「削がない」ことこそが使命。

人類はいつまでも
一体何を難しがっているのか┐(´д｀)┌

または、皆難しいフリをしていることに
吾が気がついていないだけ？

累計出荷推移

3ヶ月間の猛暑である

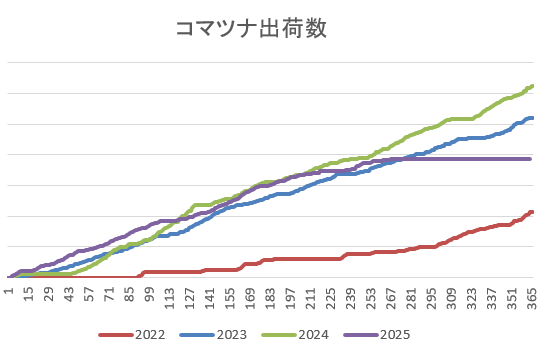
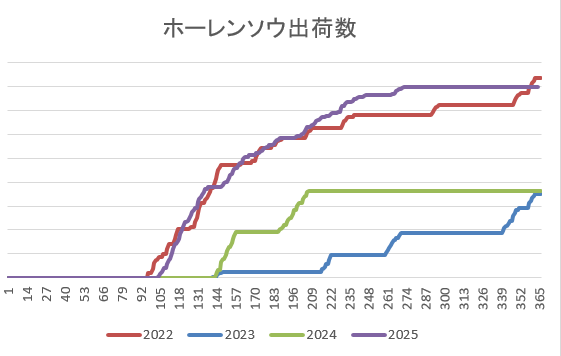
ホーレンはいまだテスト運用・数量低調とはいえ、遮光・細霧冷房が効いて、ほぼ切れ目なく出荷できた印象。例年通り雑草対応に疲弊。

コマツナは夏場ホーレン栽培の保険として設定したにも関わらず、遮光がない部分について出芽・生育不安定となり保険能力0点。

課題

ホーレン圃場の雑草

コマツナ圃場の暑熱対策

課題に対する策の有無

雑草に対しては確立済み。8月後半から検証中。

コマツナ圃場の暑熱対策については、構想済み。部材の選定中。

いずれについても、ポジティブな着地がイメージできている。

予実達成率

30％

課題

• 酷暑対策
• 豪雨対策
• 播種機対策

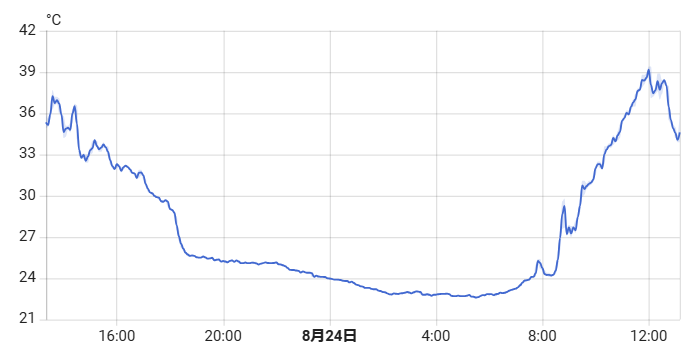
どーりで暑いはずです。一回39℃タッチしてんじゃんかorz

どうなってんだよ…　あちーなぁ

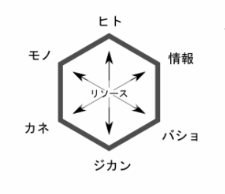
難しい算術は述べませんし、語れません。論文書いみてよエラい人

• 「微分」＝「傾き」ですよねという確認がしたいだけ
• 「成長」＝「積分」だよねという確認がしたいだけ
• 前項で云った目的に向かう垂直の矢印は、各リソースから得られる偏微分方程式の「近似解」だよねという確認がしたいだけ

各リソースは、時間に関しての関数であって、
その量や質が刻々変化しうる存在であることを、知って腹落ちすべき。

カネしか見えてない人は、「カネの質？」だろうし、耐久消費財しか見えてない人も、質の変化には鈍感だろう。直感的には物理的な距離の遠近で、その感度が変わるような気がしていますが、連続的か離散的かを問わず、時間方向に量・質は変化します。

在るときには自由自在に差配できるが、無いときには無い。

変化するのだから、それはどのように変化するのか、どのようなグラフを描く関数なのか、知らなければならない。

• １００万回あるいは１０年～１００年、現状が続いたならば（＝統計的観点で）
• 量がどのように時間変化するのか
• 質的がどのように時間変化するのか
• 予測可能な関数なのか、線形か非線形か
• 直線か曲線か、確度が高い周期性があるのかどうか