リソースって何よ論Ⅱ：微積分あるいはフーリエ解析の観点

難しい算術は述べませんし、語れません。論文書いみてよエラい人

• 「微分」＝「傾き」ですよねという確認がしたいだけ
• 「成長」＝「積分」だよねという確認がしたいだけ
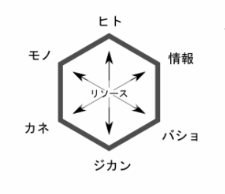
• 前項で云った目的に向かう垂直の矢印は、各リソースから得られる偏微分方程式の「近似解」だよねという確認がしたいだけ

各リソースは、時間に関しての関数であって、
その量や質が刻々変化しうる存在であることを、知って腹落ちすべき。

カネしか見えてない人は、「カネの質？」だろうし、耐久消費財しか見えてない人も、質の変化には鈍感だろう。直感的には物理的な距離の遠近で、その感度が変わるような気がしていますが、連続的か離散的かを問わず、時間方向に量・質は変化します。

在るときには自由自在に差配できるが、無いときには無い。

変化するのだから、それはどのように変化するのか、どのようなグラフを描く関数なのか、知らなければならない。

• １００万回あるいは１０年～１００年、現状が続いたならば（＝統計的観点で）
• 量がどのように時間変化するのか
• 質的がどのように時間変化するのか
• 予測可能な関数なのか、線形か非線形か
• 直線か曲線か、確度が高い周期性があるのかどうか